Tag Archives: calibration

Sync RTC time to a GPS & Setting the DS3231 Aging Offset Register to Reduce Clock Drift

Here the UNO supplies 5v to the (regulated 50mA) NEO6M and 3v to the RTC. The 5v UNO has no trouble responding to 3v signals from the Neo & RTC without level shifters. White wires to D11/D12 are GPS Rx&Tx via SoftwareSerial. The tantalum caps just stabilize the supply voltages which tend to be noisy on breadboards.

So far in 2024 we’ve released DIY calibration procedures for light, pressure & NTC temperature sensors that can be done without expensive reference equipment. Important techniques; but with long environmental time-series the 500 pound gorilla in the room is actually time itself. Precise timekeeping is something of a back-burner issue in the hobbyist world because so few are trying to combine data from multi-sensor arrays. And syncing to an NTP server is easy when you are already using wireless coms – provided that’s ‘good enough’ for your application. However for people who want high accuracy, using NTP is like setting your watch by constantly asking a friend what time it is.

An extension antenna is required or the GPS will never get a signal indoors. With that mounted in a skylight window **the** **FIRST fix** **took over 30 minutes** to acquire. Subsequent fixes took two minutes or less. It will be interesting to see how this $15 combination performs when we service loggers at heavily forested field sites.

Reconstructing a sequence of events in a dynamic earth system is challenging when timestamps are generated by independent and unsynchronized clocks. But our loggers get deployed by the dozen in underwater caves, and even when you are above ground wireless isn’t really a long term option on a single Cr2032. For stand-alone operation we rely on the DS3231 RTC as they usually drift about 30 seconds per year – but there are always a few outliers in each batch that exceed the datasheet spec of about 5 seconds per month (±2ppm) for the -SN and 13 sec/m (±5ppm) for -M (MEMS) chips. These outliers are hard to spot with our usual ‘by hand’ time-setting process over the serial monitor. You can get a set of loggers within 80 milliseconds of each other with that method, but that difference is still annoyingly visible when the LEDs pip. That set me hunting for a better solution.

Paul Stofregens TimeSerial is often suggested but TimeLib.h didn’t play well with the RTC functions already in our code base. Even after sorting that out, and installing Processing to run SyncArduinoClock, I was still initiating the process. So TimeSerial didn’t get me any closer to the perfectly synchronized LEDs I was after.

This NEO-6M module doesn’t have a PPS header, but the indicator LED is driven by the time-pulse to indicate sync status. This provides one pulse per second, synced at the rising edge, for 100msec. Soldering a jumper to the limit resistor lets you to bring that signal over to the UNO with a male Dupont header pin.

SergeBre’s SynchroTime seemed like an all-in-one solution. But even after a decade working with the Arduino IDE, I still made every newbie mistake possible trying to compile that C code for windows. There are simply too many possible editor/ compiler/ plugin combinations to sift through without a lot of mistaken installations, removals & re-installs. I wasted a couple of days before realizing that code was packaged for the QT environment, and when I saw the additional cost I finally had enough. In the end, it took me less time to build my own GPS time-sync code than I spent trying to compile SynchroTime. That’s an important lesson in the difference between something that’s technically open source and a useable solution. Of course I can’t write that without wondering how many feel the same way about this project.

Jump links to the sections of this post:

Step 1: Determine the Optimum Aging Offset

Ds3231 Datasheet pg7: **In the ideal case** there is no better option than leaving the offset at zero. However, many chips in circulation don’t match this spec: especially the -M chips which can require offsets of (-)40 or more to match a GPS pulse at room temperature. **Most of the M’s are slow**, needing adjustments from (-)20 to (-)30 at room temp, while most SN’s are usually between -10 and 0, with a few SN’s running fast.

Despite those setbacks, I couldn’t give up this quest knowing that HeyPete had achieved a drift of only 26 seconds with DS3231 offline for 3 years. The key to that spectacular result was tuning the Aging Offset Register before the run. Positive values in this register add capacitance to an array, slowing the oscillator frequency while negative values remove capacitance and increase the main oscillator frequency. The change is different at different temperatures but at 25°C, one LSB adjusts by approximately 0.1ppm(SN) or 0.12ppm(M). The exact sensitivity is also affected by voltage and age so it can only be determined for a given chip empirically. The datasheets also warn not to run noisy PCB traces under the RTC that might induce capacitive/coupling effects on the crystal but many modules on the market ignore this. My ‘rule of thumb’ when servicing loggers in the field is that changing the aging register by ±3 will correct approximately 1 second of clock drift per month when I don’t have access to the resources described in this post. Of course that requires you to have good field notes so you can be sure when the logger’s clock was last set.

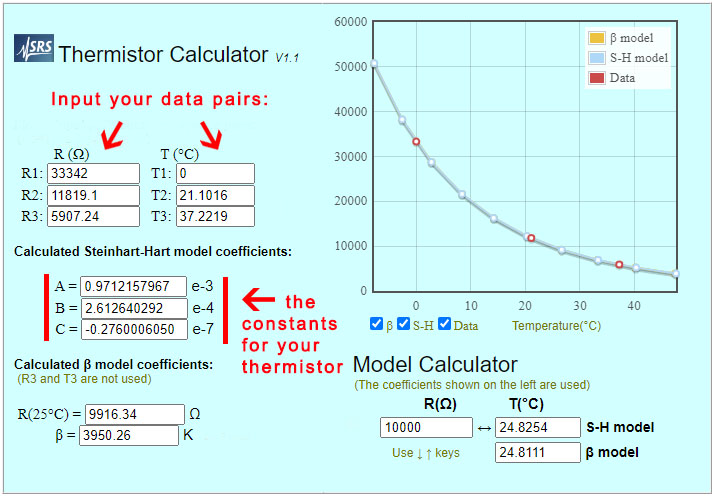
In April 2023, ShermanP proposed a method to do this using successive approximations via the Arduino system clock. After considering, and then rejecting, NTP & WWVB, he settled on GPS as the best source and then posted a ready-to-run solution on his GitHub repo: https://github.com/gbhug5a/DS3231-Aging-GPS

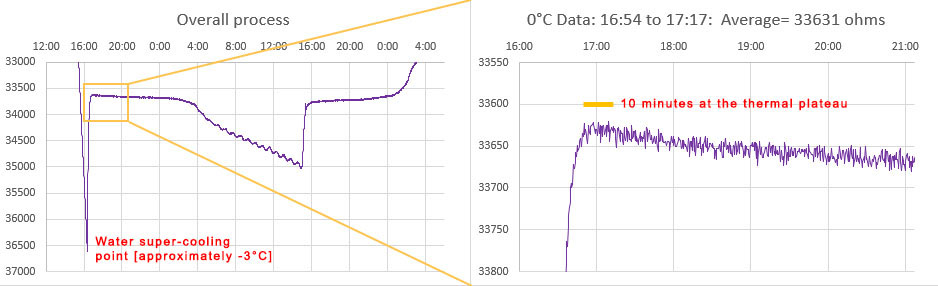
Before proceeding further, read the PDF to understand how his code works. The key idea is that “In calibrating the optimum Aging setting, you should duplicate as nearly as possible the power supply voltage the RTC will experience in its application.” although I suspect this is less critical for the crystal based -SN chips than for the MEMS oscillators. Unfortunately battery voltages change significantly with temp. so matching the rail implies you are also doing this RTC adjustment at temps near your expected deployment ranges – which may not be possible. The Cr2032s that power our loggers spend most of their operating life at 3.05v, and the power indicator LED on raw RTC modules pulls enough current that it drops the UNO’s 3.3 volt line down to about 3v. Finished loggers draw only 1-2μA while sleeping so for those I have to add a Schottky 1N5817 inline to drop that supply down to 3.05v during the test.

The rig can be used to test single RTC modules…
[this photo shows the GPS PPS connected to D3]

or finished loggers – provided – you **put the ProMini to sleep**, or load it with blink **so it ignores the I2C traffic** sent from the UNO. So we can do these tests & adjustments to loggers at any time after they have gone into service.

Sherman’s code uses the Interrupt Capture Unit so the PPS signal from the GPS must be connected to D8. I put a male Dupont pin on the end of the PPS tap so the UNO connection can be moved easily as the other code in this post requires that connected to D3. When testing the RTC inside assembled loggers, I have to use an alligator clip ( in green above ) for the alarm line which already has a soldered wire connection – so a female Dupont will not fit over that header pin.

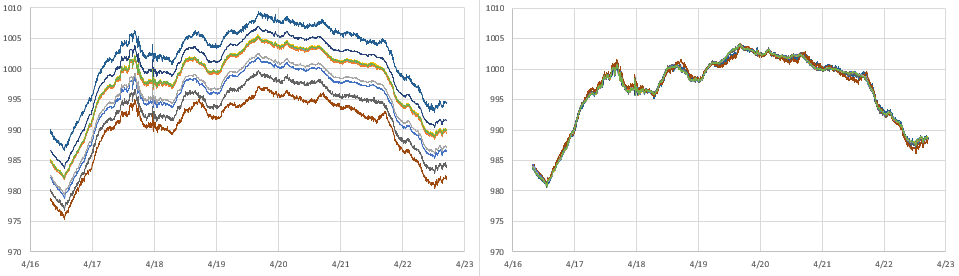
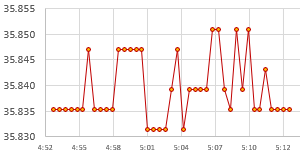
It usually takes 20-30 minutes for the adjustment on a -SN chip to reach a stable value, or settle into a pattern toggling the last bit up and down:

Each cycle of Sherman’s code shown above takes five minutes. The test tends to work better when the RTC time is close to actual GPS time, however the test changes the RTC time during the cal process. So you will need **re-sync your RTC time to the GPS** after the Age offset determination is run. In **our version**, I’ve added RTC temperature and tweaked the formatting so that it’s easier to graph the output from longer tests. But these are trivial changes.

On this (typical) -M RTC, it took an hour before the 5-minute cycles settled to a stable offset. Later runs of this unit with calcSlope() showed slightly better behavior with a value of -17 but this test might have settled there if I’d left it running longer. Averaging values from the second hour might be the best approach and you want stable temperatures so the RTC isn’t doing TCXO corrections during the test.

Unfortunately the DS3231 has no non volatile memory which means all registers will reset whenever the chip loses power. So I write the optimum offset from this test on the modules battery holder with a white paint marker during the component triage I do before building new loggers. About 2/3 of time I get very similar results when running this test on a completed build that I got from the RTC module by itself before the logger was assembled. However for about 1/3 of the RTCs, forcing the chip to run in low-power mode from Vbat slows down the main oscillator speed up to 2ppm – so the only safe approach is to retest the age register test after assembly. The BBSQW battery power alarm enable (bit 6 of the 0x0E register) must be set when running the RTC on Vbat.

Many have speculated that there are ‘fake’ DS3231 chips in circulation, but with so many showing scratches & scuff marks I suspect the bad chips are actually the result of rough handling during rework/recycling. And with a chip that’s been in production this long, some are bound to be decades old.

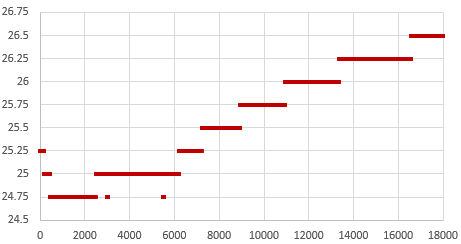
SN chips usually settle to a stable offset value within 2-3 cycles but it can take an hour or more before the -M chips produce stable age offset results. About one in 40 of the RTC modules does not settle to a consistent number no matter how long you leave it and I toss those as defective. Occasionally this is because even with the Age register pushed all the way to a max value (±127) the RTC still can not match the GPS pulse. Some of the non-calibratable units have a non functional register – you can write a value to the register and read it back but that has no effect on the output. I suspect that many of these failures are due impact damage after the chip has been dropped. I also reject any RTC where the temperature register is off by more than 3°C because they won’t be able to do the TCXO corrections. The aging register and the temperature adjustments get combined at the load capacitor bank to tweak the main oscillator, so aging register changes won’t get applied until the next (64 sec) temperature correction unless you also trigger a manual conversion. Just by chance, about one in 25 of the -SN chips keeps almost perfect time compared to the GPS with the register left at the zero default. For now I’m keeping those aside as secondary reference units.

**Units per Bin** VS **Aging offset to match GPS pulse: 140(M) & 85(SN) RTC modules**. These were selected at random from multiple eBay vendors, and tested as unmodified modules powered through Vcc at 3.05v. Six of the SN’s had zero offset and I divided those equally into the ±5 bins. Interestingly, **while the SN’s are much better behaved as a group, that chip type also had the most extreme outliers** with about ten either DOA/unstable or requiring extreme adjustment. I suspect crystal damage explains this observation as there was only one DOA in the batch of M chips.

To leave room for a decent range of TCXO correction, and with ±2ppm short-term wander (on the Mems chips) the aging register should only be used to compensate for about 6-7 ppm of baseline offset. I try not to use a module where the aging register correction to match the GPS is more than ±50.

Step 2: Synchronize RTC time with a Neo6M GPS

Most clock projects use NTP, but there are a few that go that extra mile and synchronize to GPS. One that caught my attention was: Super-Accurate GPS-Corrected RTC Clock – without Internet NTP He avoided the serial bus latency of those pokey 9600 baud coms by preloading variables with GPS time +1second and then waiting for the next GPS pulse before setting the RTC registers. With this concept in hand, and TinyGPS++ to parse the NMEA strings, it didn’t take long to whip up my own version for our loggers. It’s worth noting that several forums mentioned NMEA messages can exceed the 64byte buffer in SoftwareSerial so I increased this to 128 bytes by editing the file at: C:\Program Files (x86) \Arduino \hardware \arduino \avr \libraries \SoftwareSerial \src

Another hidden gotcha is that GPS time can be out by 2 or 3 seconds until it receives a ‘leap seconds’ update which is sent with the Almanac every 12.5 minutes. So wait until the sync LED has been blinking for 15 minutes before setting your clock time as I don’t (yet) have an error catch for this. Our RTC time-sync code displays how much adjustment was done to the RTC time and checks the latency between the GPS pulse and the new RTC time immediately after the sync. That difference is often less than 30 microseconds, but it increases from there if you leave the system running:

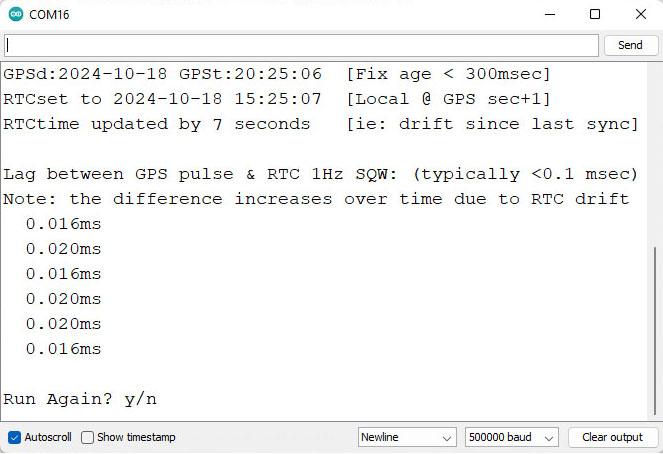
**Note:** If you just ran the aging register test in Step1 you will need to **move the PPS signal jumper from D8 to D3 before running** **RTC2_SyncDS3231Time2GPS** The RTC alarm output stays on D2. Occasionally the process spans a transition, so if you see the RTC seconds at anything other than GPSsec+1, de-power the rtc and run it again. The RTCs internal countdown only restarts if the seconds register gets *changed*, so multiple runs will not reduce the lag once the time has been synced. For some reason I haven’t identified yet, the 1Hz output from -M chips often ends about 1 millisecond *before* the GPS pulse, producing a negative lag value after sync (because the first ‘partial’ interval is too short?)

You still have to edit the code by hand for your specific local-time adjustment but everything is well commented. Most scientists run their loggers on UTC which matches GPS default time so that local time tweak can be commented out.

The external antenna connection was pretty flakey until I secured it with hot glue.

One small issue with having to run these test utilities with the RTC at 3.05v is that you’ll need to change the battery before deploying the logger. To preserve the clock time, connect the logger to a UART so the RTC is powered continuously during any battery swaps. After the time-sync & new battery, the normal procedure is to load a logger with its deployment code which has a start menu option to set the RTCs aging offset. This gets saved into the 1k EEprom on 328p processor and once set, the base-code automatically reloads that value from the EE into the RTC’s aging register at each runtime startup. After that’s done the logger is ready to deploy – so Step 3 below is only for those who want to explore the DS3231 RTCs drift behavior in more detail.

Step 3: Testing and Verifying Clock Drift

Now that we have the aging offset, and the RTC is synced to GPS time, how do we verify what we’ve done?

**HeyPete ran multi-unit drift tests** on the same breadboard with all of the RTCs responding to a single I2C master. I’m tempted to try this approach to drift testing of the other sensors like the BMP280, or the BH1750 although I might need to add a TCA9548 I2C multiplexer.

One method is simply to run the clocks until the drift can be easily measured – but that can take several months. You can get immediate results by enabling the 32kHz output on a DS3231-SN and comparing that to a high accuracy source with an oscilloscope. Ideally, you calibrate to a traceable standard which is at least one decimal place better than your device resolution. Kerry Wong did this with an HP 5350B Microwave Counter and HeyPete uses a Trimble ThunderBolt Timing GPS. There are a few retired engineers out there with universal counters on the bench and for truly dedicated ‘time-nuts‘ only an atomic clock will do. But even then the times from several must be averaged to arrive at a published value, and whenever you achieve better numbers by averaging multiple measurements you obscure potential issues with jitter.

Even if we had that equipment budget, our loggers supply the DS3231 from Vbat to save runtime power which disables the 32kHz. And -M chips don’t support that temp. compensated output no matter how they are powered. So is there any validation test that can be done without expensive kit or the 32khz line?

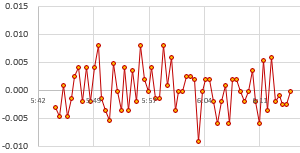
Actually there is – thanks to the Needle Nose Pliers blog in Tokyo. He developed a method that uses least squares over one minute of aggregated readings to resolve rates of change below 0.02μs/second despite the fact that an UNO sysclock only ticks at 4μs. I wrapped his calcSlope() function with modifications needed for the UNO/NEO6 test rig used here and added an input to change the Aging register before each run. To run the drift checking code from our Github, connect the GPS PPS to D3, and RTC SQW to D2:

**Note:** drift in ms will increase over time and the ppm values typically vary by ±0.02 (or more for -M chips). 9.999 indicates that the code is still collecting the initial 60 readings required for slope calculation. It usually takes another minute after that for the ppm readings to settle. The 1-second cycle-count lets you know the test duration if you leave a long test running in the background.

Once the initial 60 readings are gathered, the ppm drift calculation can be done. In real world terms, **±2ppm is about 175msec of drift per day** **and you can see that happening in real time with this output.** In the test shown above I was deliberately using an offset far from the one suggested by the Step1 test to see how much that increased the drift rate.

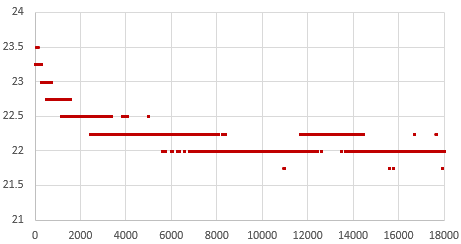
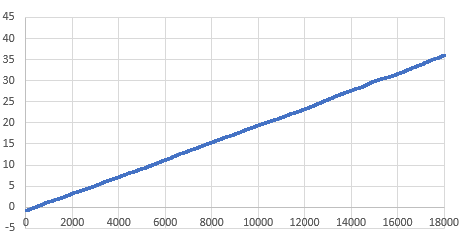
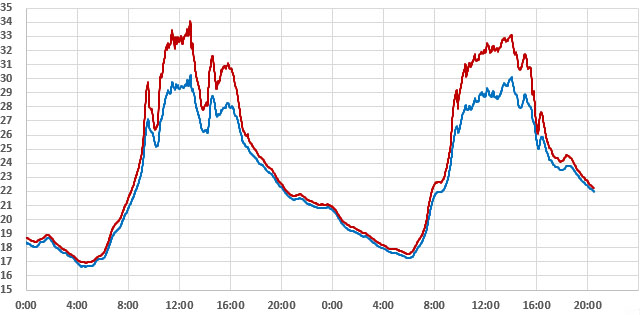
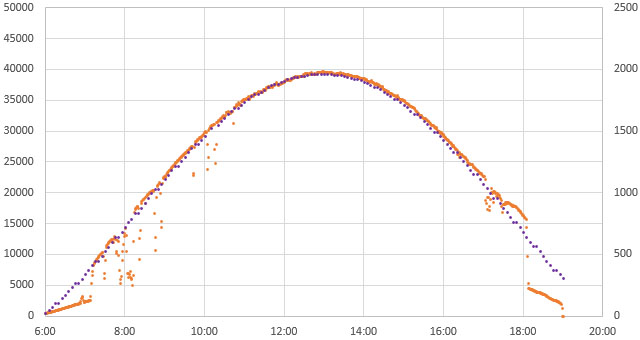
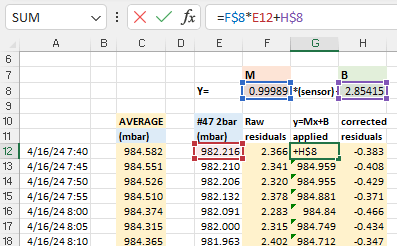
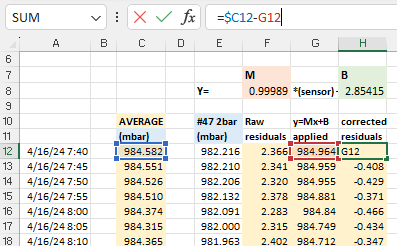
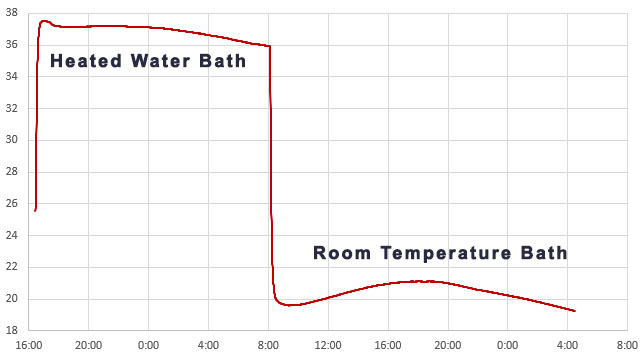
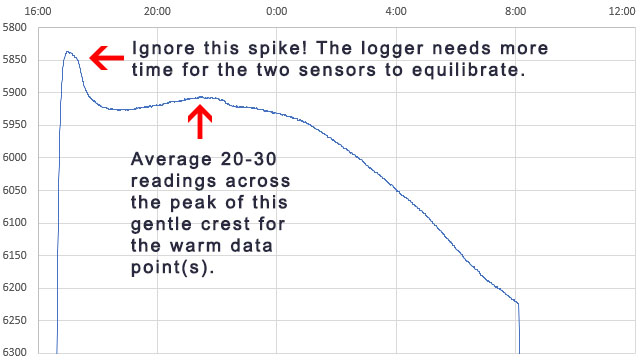
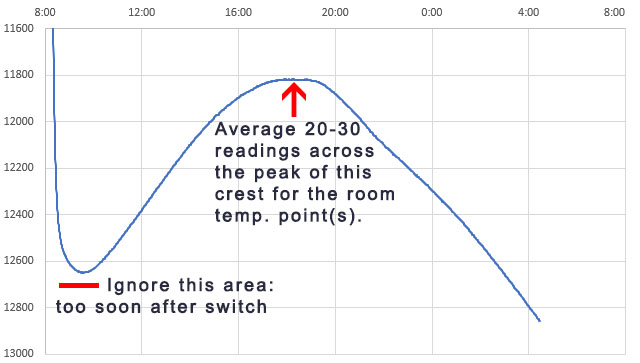
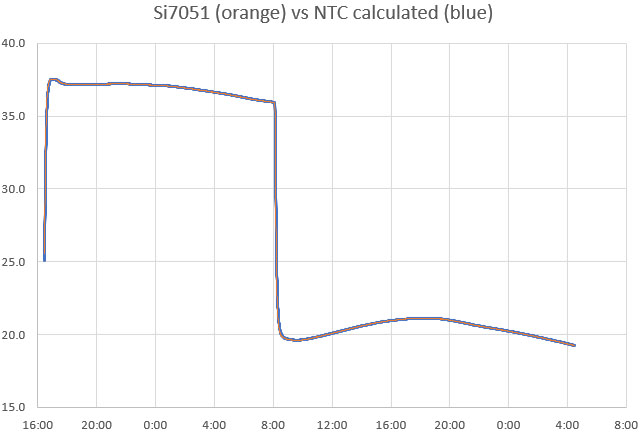
That serial output can then be copied into a spreadsheet to compare the effect that different aging offsets have on the RTC. Here are the results from two five-hour tests of a DS3231-M; first with the the Age register set at zero and then with it set to -17. The clock time was sync’d to GPS time before each test to make the graphs easier to compare with the x axis is seconds: (click to enlarge)

RTC temp. during test —> Msec offset from GPS —> Drift Error PPM

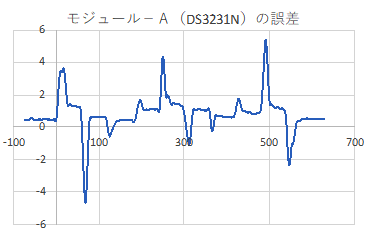
*Average* error: +2ppm (with ±2ppm jitter)

At the Age=0 default, this RTC’s 1Hz output was 35 milliseconds behind the GPS pulse after five hours, which would be roughly equivalent to 100 seconds of drift per year. The average error hovered around +2 ppm. This is well within spec for a -M chip as ±5ppm implies up to 155 seconds of drift per year.

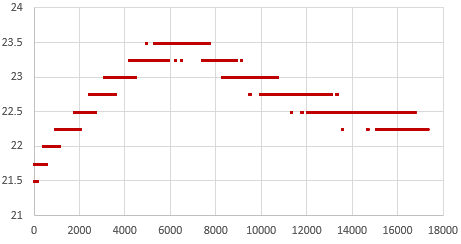
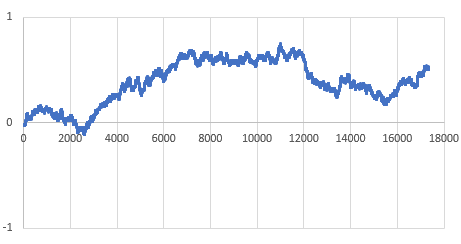
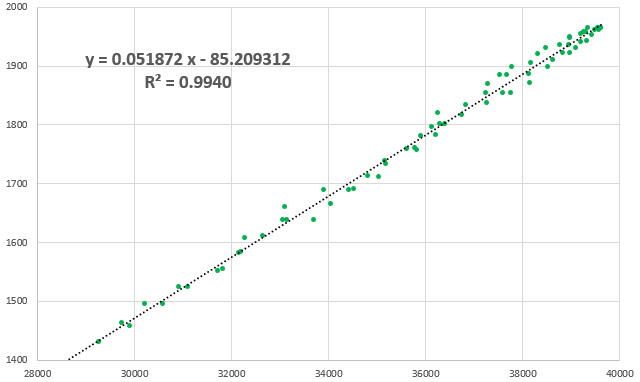
Then the Aging register was set to -17 (as determined by the test from Step1) and the drift examination was done again. That same RTC module was now only 0.5 milliseconds behind the GPS pulse after five hours, with the slope-derived error averaging close to zero ppm:

*Average* error: close to 0ppm (but jitter is the same ±2ppm)

So with the correct aging offset this -M chip could be expected drift less than a second per year. Of course this only applies near our Step1 testing temperature, but in general: If you found the best aging offset correction, the msec difference between a 1Hz alarm from the RTC and the GPS pulse should change very little over a short test.

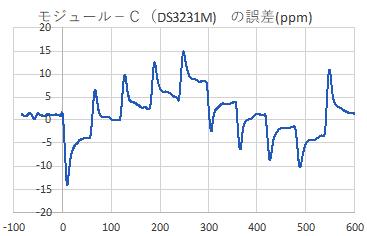
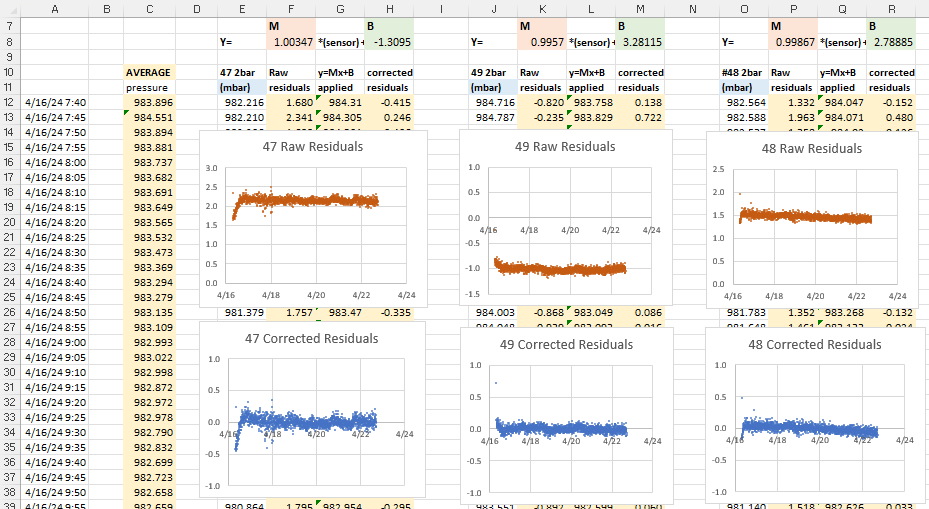
Its worth noting there is ±2ppm of jitter in the calculation with that -M chip (above) that is not present for -SN chips. The -SN shown below had a straight linear drift of 20 milliseconds slow over five hours when its Aging register was left at the zero default (that’s about 35 seconds/year or 1ppm), but the same RTC had near zero milliseconds of drift over five hours when the aging offset was set to -21:

Msec drift approaching zero after 5h, with TCXO adjustment.

Error ppm ~0, with **very little jitter on this -SN** chip

**Error(ppm) vs Runtime(sec):** This drift verification on a DS3231-M was done with an age offset of -33 from the Step1 test. The B term in the Excel linear trendline fit is less than the 0.12ppm/bit register adjustment, confirming that -33 is optimal for this chip. The absolute timing change over this 2.5h test was less than 1/2msec faster than the GPS pulse.

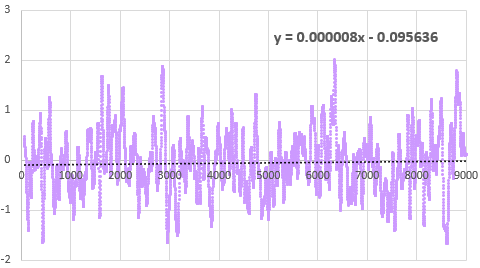
Even with temperature rising 3°C during the test, that -SN stays within a tighter tolerance than the -M. This difference in short-term variability explains why the offset determination settles so quickly with a -SN, but can wander around for some time with a -M. The code used here in Step3 is like a slow verbose version of what’s being done in step1 that shows all the intermediate readings. If you put a linear trendline on the graph of the error PPM from running this test with the offset left at the zero default, you can estimate how much age register adjustment it would take to shift those readings until the average is near zero. The aging offset suggested by the test in Step1 should be close to the result of dividing the ‘b’ term from the y=mx+b trendline fit equation by 0.1ppm(SN) or 0.12ppm(M), and changing the sign.

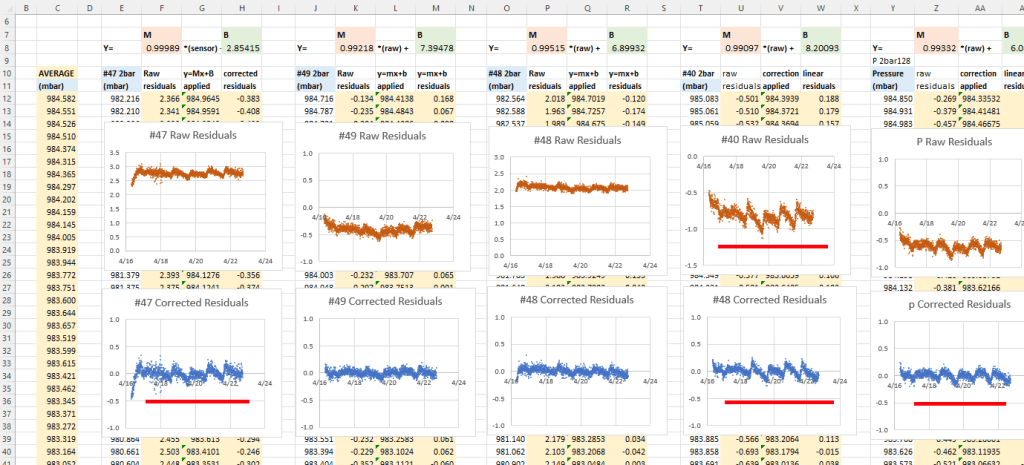
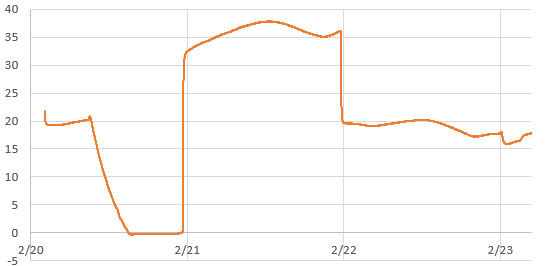
On his blog, NNP also demonstrated how the two chip variants have different responses to temperature changes:

The RTC on a Peltier temperature controller.

**Temp(°C) vs Time(sec):** The RTC modules were exposed to this overall pattern although the final tests were run faster (blue = program, orange = PID actual)

**Drift Error** (ppm) **vs Time** (sec): The spikes are due to the fact that the TCXO corrections only occur every 64 seconds on the -N variant, but after that the chip quickly returns to its ±2ppm spec.

While still within the rated ±5ppm the -M shows greater variability. With the -M chips doing corrections every 10 seconds I’m surprised the *overall* TCXO response takes a longer.

[ images from: http://radiopench.blog96.fc2.com/blog-entry-960.html ]

This confirms what I already suspected from our data: the -SN chips are a much better choice for outdoor environments where temperatures vary over that entire 50°C range. Although the temperature coefficient of the MEMS oscillator is not specified in the datasheet, loggers built with -M chips are probably still fine for stable thermal environments and with a tuned Aging register I’d expect them to drift less than ten seconds per year indoors. There are other insights if you dig into NNP’s blog. For example, drift is also affected by the physical orientation of the chip with respect to gravity. I had no idea it was a problem for all quartz resonators unless the crystal is cut into a special shape to avoid it. This highlights the fact that with so many different factors affecting the RTC, the Aging offset adjustment will never be perfect; you are simply aiming to reduce the ‘average’ drift. These tests are also affected somewhat by the stability of the oscillator on the UNO so we have a chicken & egg thing there.

I will be doing more tests to see what other insights it can give into our ProMini / DS3231 combination. With the ability to synchronize clocks so precisely (in Step 2) you can see the outliers in a group in as little as 24 hours simply by watching the LED blinks. I already do multiple rapid burn-in tests with new loggers as part of pre-deployment testing, so visually checking synchronization during those runs is low-effort way to verify the RTC. One thing I’ve long suspected, but have never seen any actual proof of, is that the process of updating registers and generating alarms also affects the clock time. Perhaps handling the I2C transaction blocks the update of some internal counter? I could test this by setting one logger in a ‘well matched’ group to wake every second, while the others blink at five seconds, and see how many days it takes for the fast blinker to shift out of alignment.

It would be interesting to get a couple of the newer DS3232 / DS3234 chips, and test how much they drift with their TXCO pushed out to 512 seconds for 1µA current, instead of the 64 second default that pushes the DS3231’s up to about 3µA average standby current.

Last Word

With these three tools to wrangle our time series we could see drift as low as five seconds per year from an SN in a stable environment, so our little 328p loggers can finally go toe-to-toe with all those smugly networked ESP32s. I will eventually combine these into a general RTC testing utility, but there are plenty of use cases for each as an isolated step – especially if you were tweaking the code for use with different RTC chips. Likewise, with the Neo being a 3v device I could add a few header pins to our loggers for the serial coms and run everything with the logger alone.

But I’m somewhat sentimental about the original UNOs, so it’s nice to dust them off once and a while. Another factor is that if you run two separate instances of the IDE you can choose a different com ports for each instance. So you can simultaneously have that UNO/GPS combination connected, and a ProMini logger connected via its own UART module. As long as you align the code open in each instance with the appropriate port, you can run those RTC tests on the UNO in the background while you work in the other instance of the IDE. This will be very handy when servicing loggers in the field. I will secure those field calibration rigs with hot glue and make them more compact with a ‘sit-on-top’ protoshield.

The quid pro quo when adjusting the Aging register is that the reduced drift within the tuning temperature range comes at the cost of increasing non-linearity at more extreme temperatures. But the underwater/cave sites we deploy into are quite stable compared to surface conditions, so it’s probably worth the trade. Physical aging rates are not necessarily constant or linear, so I expect that that register will need a yearly update. The first complete generation of fully sync’d & calibrated RTCs will get deployed this fall, so it will be a while before I can check how aging is changed by exposure to real world temperature variation. I’ll be happy if I can get -M’s below 1 second of drift per month under those conditions. I would hope to see the aging stabilize after the first year of operation, in a manner similar to sensor aging.

At the very least, we’ve greatly enhanced our ability to remove any duffers from those cheap eBay parts. I’m still wondering what new sensor possibilities better time discipline might enable but I can already see some interesting labs for the next cohort of e360 students. One of the more challenging things to demonstrate within the constraints of a classroom is the relationship between datasheet error specifications and sensor drift. I’ll set aside a few -M modules for those teaching loggers so the results are more dramatic.

References & Links

Using a $1 DS3231 Real-time Clock Module with Arduino
A look inside the DS3231 real-time clock by HeyPete
5 Month DS3231 Drift Results at HeyPete.com
Setting the DS3231 Aging register to an optimum value by SermanP
Super-Accurate GPS-Corrected RTC Clock without NTP
Precise measurement of RTC error using GPS from Needle Nose Pliers
How they test Aging Performance in Crystals from Connor Winfield
Choosing the right RTC at Hackaday & module photos at Craft Corner
Comparing DS3231 / PCF8563 / MCP79400 / DS1307 RTCs
A collection of very detailed RTC tests from Dan Drown
And his GPS module measurements Part1, Part2, Part3 and More
An architect’s guide to GPS data formats, Estimating GPS time to FIRST fix
The U-centre program from u-blox, with multiple displays
Can the 60Hz mains frequency be used as a reference?
A Timing-sync Protocol for Sensor Networks
PTP clock synchronization over a WAN backbone
Arduino system clock accuracy [ ±1000ppm], various crystal error specs
RTC seconds/day to ppm drift calculator

Just adding a reminder here: the DS3231 doesn’t have a built-in mechanism to disable alarms after they’ve been set. You can clear the alarm flag to release SQW after it fires, but the alarm will still be armed and will fire again at the next time match – no matter how you set the ‘enable/disable’ bits. The ONLY way to disable alarms on the DS3231 is to load those registers with an ‘invalid’ h/m/s combination that the actual time can never reach (eg: one with minutes/seconds set to 62 or, date set to Feb 31st). You can also set the EOSC bit of the control register to logic 1 which stops the oscillator when the DS3231 is on VBAT power – but you will then be unable to check the clock drift at the next logger download. Halting internal oscillator is the only way to stop the temperature conversions.

From the data sheets you can see that the -M uses half as much power (about 26 milliAmpSeconds/day) as the -SN chip does (45 mAs/d) to do its TXCO corrections however our standard Promini/DS3231-SN module combination usually sleeps around 890 nA while the same logger built with a DS3231-M will sleep closer to 1680nA (when a temp compensation reading is not occurring). A sleeping 328p based ProMini draws ~150nA (reg removed & BOD off) and the 4K AT24c32 EEproms on the modules draw less than 50nA when not being accessed. So the -M chips have more than 2x the ~700nA Ibat timekeeping draw of -SN chips.

How to measure PAR (Photosynthetically Active Radiation) using a BH1750 Lux Sensor

A 3d printed stack of radiation shields goes around the 30mL centrifuge tube housing our **2-module logger**. A universal ball joint by DiZopfe was adapted for the leveling mechanism which is critical for the calibration.

Space nerds have an old saying that ‘LEO is half way to the moon…‘ and Arduino hobbyists tend to feel the same way about getting sensor readings displayed on a live IoT dashboard. But that ignores the real work it takes to generate data that’s actually useable. To paraphrase Heinlein: ‘Calibration is half way to anywhere…’ Now that our 2-Part logger is both easy for students to build and robust enough for field use, we can focus on developing sensor calibration methods that are achievable by teachers and researchers in low-resource settings.

Light sensors seem straight forward, with numerous how-to guides at Hackaday, Adafruit, Sparkfun, etc. In reality, light sensors are some of the trickiest ones to actually deploy – which is why so few low-end climate stations include them. This post describes a method for calibrating a Bh1750 lux sensor to estimate Photosynthetically Active Radiation (PAR). Not everyone can afford a LI-COR 190 or Apogee SQ quantum sensor to use as a benchmark, so here we will use a clear-sky model calculation for the cross-calibration despite the dynamic filtering effects of the atmosphere on natural sunlight. Using a diffuser to restore cosign behavior means we can’t calculate PPFD directly from Lux without some y=mx+b coefficients.

Jump links to the sections of this post:

Light Sensor Issue #1: Changing Spectral Distribution

Solar irradiance spectrum above the atmosphere and at ground surface

Peak solar irradiance received on any given day varies by latitude and season, as does the overall pattern. Light emitted from the sun has a stable distribution of frequencies, however the spectrum at the earth’s surface varies across the day, with more short wavelengths (blue) around mid day and enriched in longer wavelengths (red) at sunrise & sunset when the rays travel further through the atmosphere. We will avoid this source of error by calibrating with data from the hours around solar noon as determined by the NOAA Solar Calculator. Even with high quality sensors, morning and evening data can be compromised by other factors like condensation which changes the refractive index of lenses and diffusers.

Light Sensor Issue #2: Sensitivity Bands

Average plant response to light as Relative Photosynthetic Efficiency (%) vs Wavelength (nm) compared to Bh1750 Response Ratio vs Wavelength

Lux sensors have a maximum sensitivity near 550nm, mimicking the response of photo-receptors in the human eye. Plants are similarly limited to frequencies that can be absorbed by the various chlorophylls. These two bands have a high degree of overlap so we can avoid the Badder UV/IR-Cut cut filters (420–685nm bandpass) or stack of Roscolux filters that would be needed with photodiodes that respond to a wider range of incoming radiation. The cross-calibration still requires the relative ratio of frequencies within the targeted region to remain stable, so a PAR conversion derived under full sunlight may not be valid under a canopy of tree leaves or for the discontinuous spectra of ‘blurple’ grow-lights.

Light Sensor Issue #3: Dynamic Range

I tested two inexpensive Bh1750 sensor modules, and **the diffuser dome that comes with the red ‘Light Ball’ version turned out to be the deciding factor.** When powered from a 3v coin cell, these sensors add 8µA to the loggers sleep current if you leave the 622 reg in place and <1µA if you remove it.

Full summer sunlight can exceed 120,000 Lux and there aren’t many sensors in the Arduino ecosystem that handle that entire range. The BH1750 can with registers set to it’s least sensitive configuration. Our logger code already does this because QUALITY_LOW & MTREG_LOW(31) integration take only 16-24 milliseconds, rather than the 120-180ms of power needed for high resolution readings. The data sheet implies that the sensor will flatline before 100,000 lux, but at its lowest sensitivity it delivers reasonable data above 120k, though linearity may be suspect as flux approaches sensor saturation. The sensor also has a maximum operating temperature of 85°C which can be exceeded if your housing suffers too much heat gain. Alternative sensors like the MAX44009, TSL2591 and SI1145 have a similar thermal limits. Like most light sensors, the Bh1750 increases its output readings by a few percent as the sensor warms.

Commercial vs DIY diffusers. Bullseye level indicators are epoxied to the top shield with white JB Marine Weld. The larger 43mm diameter bubble (right) was far more effective than the smaller 15mm (left).

DIY builders often add diffusers made from translucent #7328 Acrylite or PTFE sheets to reduce sunlight intensity into a given sensors range. I tried printing domes with clear PETG and hand sanding them with fine grit to increase the diffusive power. While these did reduce light levels by more than 50%, my DIY diffuser didn’t quite match the smooth overall response seen with the diffusers that came with the round PCB modules. This may have been due to a slight misalignment between the sensor and the focal point of the low-poly dome I could make in Tinkercad. The white dome that comes with the red Bh1750 module reduced peak light levels in full sunlight from the 110k Lux reported by a ‘naked’ sensor to about 40k Lux. Each sensor varied somewhat in its response but I didn’t do any batch testing to quantify this as I was calibrating each sensor directly to the reference model. I initially tried clear JB weld as a sealant but this caused problems: sometimes contracting enough peel parts away from the PCB and yellowing significantly after a couple of weeks of full sun exposure. In later builds I used only a thin coating of silicone conformal, relying on an epoxy seal around the base of the diffuser to provide most of the waterproofing.

Light Sensor Issue #4: Angular Response

Bh1750 Directional Characteristics [Figs 4&5] from the datasheet. **Sensor response is different on the two axes** so orientation must be labeled on the outside during assembly. The left graph is closer to Lambertian **so the** **sensor gets deployed with its connection pads oriented North – South** relative to the suns east-west motion. Based on these curves alone we would expect a ‘naked’ BH sensor to under-report relative to the Lambertian ideal. That is indeed what I observed in our early sensor comparison tests, leading to our selection of round red PCB modules for the calibration because the included diffuser dome compensated nicely.

Lambert’s cosine law describes the relationship between the angle of incidence and the level of illuminance on a flat matte surface as being proportional to the cosine of the zenith angle (as the suns changes position throughout the day). At an incident angle of 60°, the number of photons hitting a sensor surface is half what it would be if the same light source was positioned directly above the sensor. This effect is mathematically predictable, but imperfections, diffraction, and surface reflection means that sensor response tends to diverge from ideal as the angle increases. So manufacturers surround their sensors with raised diffuser edges and recesses on the top surface which change light collection at low sun angles to restore a perfect cosign response. In general, diffusers make the compass orientation of the sensor less likely to interfere with calibration but leveling the sensor is still absolutely required.

Light Sensor Issue #5: Temporal Resolution

Unlike most environmental parameters, light levels can change instantaneously. Most commercial sensors aggregate 1 or 2 second readings into 5 to 15 minute averages. This makes it much easier to estimate energy output from solar panels, or calculate the Daily Light Integral for a crop because both of those use cases are more concerned with area under the curve rather than individual sensor readings. However, in our case of calibrating a sensor against an irradiance model, we must use instantaneous readings so we can exclude data from periods where the variability is high. Averaging would smooth over short term interference from clouds, birds, or overhead wires, potentially leading to bad data in the calibration. We read the BH1750 once per minute at its fastest/lowest resolution.

A Radiation Shield

My original concept was to epoxy the light sensor directly onto the cap and slide separate radiation shields over the housing tube with a friction fit – but that approach suffered excessive heat gain. It took several design iterations to discover that plastics are often transparent to IR – so most of the 3D printed weather station shields you find in maker space won’t work very well. While PLA does block/reflect the visible spectrum, it then re-emits a portion of any absorbed energy as IR which passes right through – turning the central housing tube into a tiny greenhouse. You need to add layers of metal foil to reflect that IR and there must be an air gap between the materials or the heat still crosses by conduction. The process of moving those surfaces away from the logger also meant placing the sensor onto a small raised ‘stage’ that could pass through the upper shield. This allows easier replacement after the sensors expire, or the use of an entirely different sensor without changing the rest of the design. I still don’t know the operating life of these sensors at full sunlight exposure levels.

2″ Aluminum HVAC tape is applied to the IR shield layer. (click to enlarge these photos)

The IR shield slides to about 8mm below the top shield which has holes along the rim to vent heated air.

The sensor stage slides on the vertical rails and passes through the upper shield.

The loggers green cap then pushes the sensor stage into place with a snug click-fit. Foil is wrapped around the logger housing tube.

Three smaller gill shields slide onto the rails, with plenty of aligned holes for vertical airflow through to the top shield.

A lower IR shield is added to the bottom with metal side down to reflect thermal radiation emitted from the ground.

Here are temperature records of two side-by-side loggers with identical 3D-printed shields except that one has the three metal foil layers added and one does not:

Temp (°C) vs Time: Comparison of heat gain with, and without metal foil layers. Measured with the NTC sensor inside the logger housing at the center of the stack. The night time data shows a 0.25°C offset between the two sensors, indicating that they were not normalized before this run.

Interestingly, the 3°C delta seen in my foil vs no foil tests matched the discrepancies identified by Terando et.al in their 2017 paper examining ad hoc Stevenson shields in ecological studies. Air gaps are required for IR reflecting layers to do their job, so most of the foil backed roofing shingles on the market are ineffective because of direct surface contact. Both aluminum and stainless steel foils are common, but aluminum has a lower emissivity than stainless steel, meaning it should reflect more and emit less IR. There are also radiant barrier coating sprays used in industrial settings. High-end weather stations use fan ventilation or helical shields, but those designs may be a bit too complicated for DIY. And even 3D prints from tough materials like PETG or ASA would benefit from coating with something like Krylon UV protectant to extend their lifespan. I’ve also been thinking about adding some infrared cooling paint on the top surface of our weather stations. The challenge with anything that emits in the atmospheres transparency window between wave lengths of 8 and 13 microns is that you get significant accumulation of debris on surfaces in as little as one month of actual deployment: especially in the spring/fall when the surfaces get covered with morning dew which then captures any windborne dust.

I’m still tweaking the shield design as more test data comes in, and hope to compare it to a fan aspirated model soon. Radiation shields are only needed if you want to capture accurate temperatures with the light readings on the same logger. The Bh1750 calibration alone could be done without shields, but mounting the sensor on some kind of flat surface makes it easier to add the required leveling bubble beside the sensor. The tradeoff for preventing solar heat gain is that shields introduce lag in the temperature response.

Pole Mount & Leveling Mechanism

As this is the first of our ‘garden series’ that will be built around the 2-part logger, I created a complete mounting system from a combination of 3D printed parts and PVC pipes. This adjustable leveling mechanism was modified from the Open Source Universal Ball Joint posted on Thingiverse by Arthur ZOPFE.

This socket slides over the end of a 1/2″ PVC pipe. A zip tie through the drilled cross-hole secures the pieces together.

A self standing 30mL centrifuge tube slides snugly into this fitting, again with holes for zip ties.

A large diameter twist ring makes it easy to adjust the sensor assembly while watching the bulls-eye level on the top shield.

This ball & socket approach works well for leveling, but to make the adjustments easier (ie. with less compressive force) I will add an O-ring to the bottom cup for some friction and give.

This ground spike has a foot plate to assist insertion and is asymmetric to provide more contact with the bed. It just barely fits on my Ender3 when printed diagonally. I created this model from scratch in Tinkercad, but the offset idea is not mine. Unfortunately, I saw the original so long ago I don’t know who to credit for it. The pole insert and holes are six-sided because internal 45° slopes can be printed without any supports, and you can simply bridge the internal 1cm top span.

A length of standard 1/2 inch PVC pipe is used for the riser between the spike and the leveling mechanism. Ideal height for temperature sensors is approximately five feet above the ground, usually in a shaded location facing away from the sun.

The Apogee Clear Sky Calculator

With this model we could even attempt a calibration against the shortwave spectrum for a DIY pyranometer, but it’s a much bigger stretch to say the 550nm peak of BH sensitivity is a good proxy for the whole 300 -1300nm band of frequencies.

The Apogee Clear Sky Calculator helps operators of their many light sensor products check if those need to be sent in for re-calibration. When used near solar noon on clear unpolluted days the accuracy is estimated to be ±4 %. We can cross-calibrate the readings from our humble Bh1750 to that model provided we use data from a cloudless day. I’m not sure what the temporal resolution of the ClearSky model is (?) The U.S. Climate Reference Network generally uses two-second readings averaged into five minute values so it is likely that the ClearkSky model has a similar resolution. This model has the best accuracy within one hour of solar noon but we will push that out a few hours so we have enough data for the regression.

We could have used the Bird Clear Sky Model from NREL, with validation against real world data from one of the local SURFRAD stations at NOAA. That data is for full-spectrum pyranometers measuring in W/m^2, but you can estimate the PAR as photosynthetic photon flux density (PPFD) from total shortwave radiation using a conversion factor into µmol s^-1 m^-2. Many solar PV companies provide online calculators for power density that could also be used for this kind of DIY sensor calibration.

Our Deployment Location

Most who live in urban areas are familiar with noise pollution, however it is also hard to find undisturbed light environments. My best option for those critical hours around solar noon was my neighbours backyard garden:

The two sensors here are aligned on the east-west axis so they can be compared.

This location was relatively free of power lines and tree tops, but reflections from that white door caused a slight positive offset in the afternoon. Fences prevented the capture of morning and evening data which would have been interesting. But sunrise to sunset data is not required for our calibration.

The Calibration

After several weeks of logger operation we finally managed to capture data from a beautiful cloud-free day:

**2024-07-27:** **Lux from a diffused ‘Light Ball’ Bh1750 sensor** (**Orange**, left axis @1min) **VS ClearSky Model PPFD** (**Purple**/right Axis @ 5min). You can see some stair-stepping in the model data, indicating that it’s temporal resolution might be only 10-15 minutes.

We logged raw single-shot Lux readings at one minute intervals and because there is no averaging applied you can clearly see where overhead lines or birds created occasional short-duration shading. These outliers were excluded before generating the trendline shown below. The PAR values from the model were calculated using the ‘Auto fill’ option for humidity and temperature. On this day solar noon was at 12:57

**Linear y=mx+b fit between ClearSkyCalculator PPFD** (yAxis) **vs Diffused BH1750 Lux** (xAxis) using 5 minute data points on 2024-07-27 between 10:00 and 16:00 [bracketing solar noon by three hours]. Two shadow outliers at 10:05 and10:15am were excluded from the dataset.

Aerosols and variations in local temp/humidity produced some scatter but this is a good result for calibration with natural light. The result might be improved by co-deploying a humidity sensor, but it’s not clear to me if humidity at ground level is what the model actually uses for its calculation. Some scatter is also being created by the temporal resolution of the model. Using one type of sensor as a proxy for another limits the scope of the device and we probably approached an accuracy of ±15% at best with this conversion. It’s worth remembering that most commercial light sensors are only calibrated to ±5%.

Discussion

The biggest challenge at our mid-west location was that we had to run the loggers for several weeks before capturing the blue-sky day shown above. Typical time series from that Bh1750 sensor (under a light-reducing diffuser dome) looks like this:

**Lux vs Time:** 1 minute data captured with our 2-Part logger reading a red ‘light-ball’ Bh1750 module.
This unit had an extra 64k EEprom added to store the large amount of data that was generated.

Clouds often cause light levels to exceed that seen on clear days. This makes sense if you imagine a situation where there are no clouds directly over-head, but radiation reflected from the sides of clouds is reaching the sensor from multiple directions. The fact that clouds at different atmospheric levels have different effects is one of the things that makes climate models so complicated.

The Clear-Sky Calculator lets you generate data for any date/time, so it would be possible to do this calibration by aggregating cloudless periods from multiple days:

**Detail of data from 7/15 and 7/12:** what you are looking for is the smooth curve that indicates there were no high level clouds causing subtle variations in light level.

Inexpensive (~$60USD) PAR meters have started appearing on Amazon recently. I’m more than a little dubious about the term ‘quantum’ in the marketing (?) as they are probably just a photodiode and some filters

Someone in Nevada would have no trouble gathering this kind of calibration data, but it might not be possible for people living in Washington. A low-cost alternative to using a clear-sky model for the calibration could be to compare the Bh1750 to one of the many smartphone grow light meter apps, with a clip-on diffuser & cosine corrector. Every phone has a different sensor so programs like Photone or PPFDapp usually have their own calibration procedures. While developing this exercise I also found a ‘for parts’ Seaward Solar Survey 100 on eBay for $20, and all it needed to bring it back to life was a good cleaning inside. I also found an old Li-1400 logger with a 190 pyranometer for only $120 and was pleasantly surprised when Apogee’s calculator showed it was still within 5%. As mentioned, you’d need to convert total radiation from those last two into PAR or you could do the calibration to total shortwave. Hardware references that lack logging capability require more effort to gather calibration points, but they save you from having to wait for agreeable weather.

Other projects have built similar sensors and with calibration Lux sensors are comparable to commercial PAR sensors if the spectral environment is consistent. Multi-channel sensors with overlapping frequencies do a better job in situations with discontinuous light sources like those used for indoor growing or for measuring the extinction of PAR frequencies under water. In those cases a TCS3471 (3-channel), AS7341(10-channel), or AS7265 (18-channel) sensor could be used, and finer frequency division can enable calculation of interesting ratios like NDVI or SPAD. Beyond that point you’re entering the realm of diffraction grating spectrometers which allow a more nuanced approach to the spectral function which differs from standard PAR.

And if building your own datalogger is too challenging, you could reproduce the exercise described in this post with a bluetooth UNI-T or a UT381 Digital Luminometer which has some logging capability. But you will need to add extra diffusers to bring full sunlight down below its 20,000 Lux limit.

References & Links

NREL Bird Clear Sky Model
Clear Sky Calculator from Apogee Instruments
NOAA SURFRAD data from irradiance measuring stations
Downloading from the National Solar Radiation Database.
Shortwave Radiation by Steve Klassen & Bruce Bugbee
Fondriest Solar Radiation & Photosynthetically Active Radiation
Designing a Low-Cost Autonomous Pyranometer by Peter van der Burgt
Various DIY PAR meter discussions at Planted Tank
Build Your Own Pyranometer by David Brooks
Ad hoc instrumentation methods in ecological studies produce biased temperature measurements. Terando et al. (2017)
Choosing Standard Bulbs for DIY PAR meter calibration
Daily Light Integral requirements for different plants.
PARbars: Cheap, Easy to Build Ceptometers
Creating a Normalized Vegetation Index Sensor with two LEDs
Hacking the Rubisco enzyme boosts crop growth 40%
Plants recycle UV into red light
How to calibrate NTC thermistors
How to build our 2-Part ProMini Data Logger

How to Normalize a Group of Pressure Sensors so they can be Deployed as a Set

Once your project starts to grow it’s common to have multiple different sensors, from different vendors, measuring the same environmental parameter. Ideally, those sensors would produce the same readings but in practice there are significant offsets. Datasheets for the MS5837-02BA and MS5803-14BA that we will compare in this post claim an accuracy of (±0.5mbar) and (±2ºC) for the 2-bar while the 14-bar sensors are only rated to (±20mbar) and (±2ºC). Sensors from Measurement Specialties are directly code compatible so the units here were read with the same Over Sampling settings.

**Barometric pressure from a set of nine MS58xx pressure sensors** running on a bookshelf as part of normal burn-in testing. The main cluster has a spread of about 10millibar, with one dramatic outlier >20 mbar from the group. **These offsets are much wider than the datasheet spec for those 2-bars sensors.**

But this is only a starting point: manufacturers have very specific rules about things like the temperature ramps during reflow and it’s unlikely that cheap sensor modules get handled that carefully. Housing installation adds both physical stress and thermal mass which will induce shifts; as can the quality of your supply voltage. Signal conditioning and oversampling options usually improve accuracy, but there are notable exceptions like the BMP/E 280 which suffers from self-heating if you run it at the startup defaults.

As described in our post on waterproofing electronics, we often mount pressure sensors under mineral oil with a nitrile finger cot membrane leading to thermal lag.

Sensors like NTC thermistors are relatively easy to calibrate using physical constants. But finding that kind of high quality benchmark for barometric sensors is challenging if you don’t live near a government-run climate station. So we typically use a normalization process to bring a set of different sensors into close agreement with each other. This is a standard procedure for field scientists, but information on the procedures is hard to find because the word ‘normalization’ means different things in various industry settings. In Arduino maker forums it usually describes scaling the axes from a single accelerometer with (sensor – sensor.min )/( sensor.max – sensor.min ) rather than standardizing a group of different sensors.

When calibrating to a good reference you generally assume that all the error is in your cheap DIY sensor and then do a linear regression by calculating a best fit line with the trusted data on they Y axis of a scatter plot. However, even in the absence of a established benchmark you can use the same procedure with a ‘synthetic’ reference created by drawing an average from your group of sensors:

Note: Sensor #41 was the dramatic outlier more than 20millibar from the group (indicating a potential hardware fault) so this data is not include in the initial group average.

With that average you calculate y = Mx + B correction constants using Excel’s slope & intercept functions. Using these formulas lets you copy/paste equations from one data column to the next which dramatically speeds up the process when you are working through several sensors at a time. It also recalculates those constants dynamically when you add or delete information:

The next step is to calculate the difference (residuals) between the raw sensor data and the average: before and after these Y=Mx+B corrections have been applied to the original pressure readings. These differences between the group average and an individual sensor should be dramatically reduced by the Mx+b adjustments:

After you copy/paste these calculations to each sensor, create x/y scatter plots of the residuals so you can examine them side-by-side:

Now we can deal with the most important part of the entire process: Normalization with bad input data will produce even more misleading results. While the errors shown above are centered around zero, the patterns in these graphs indicate that we are not finished. In the ideal case, residuals should usually be soft fuzzy distributions with no observable patterns. But here we have a zigzag that is showing up for most of the sensors. This is an indication that one (or more) of the sensors included in the average has some kind of problem. Scrolling further along the columns identifies the offending sensors with nasty looking residual plots after the corrections have been applied:

Sensor #41 (far right) was already rejected from the general average because of its enormous offset, but the high amplitude jagged residual plots indicate that the data from sensors #45 and #42 are also suspect. If we eliminate those two from the reference average the zigzag pattern disappears from the rest of the sensors in the set:

There’s more we could learn from the residual distributions, but here we’ve simply used them to prune our reference data, preventing bad sensor input from harming the the average we use for our normalization.

And what do the sensor plots look like after the magic sauce is applied?

The same set of barometric pressure sensors, before and after normalization corrections. (minus #41 which could not be corrected)

It’s important to note that there is no guarantee that fitting your sensors to an average will do anything to improve accuracy. However, sensors purchased from different vendors, at different times, tend to have randomly distributed offsets. In that case normalization improves both precision and accuracy, but the only way to know if that has happened is to validate against some external reference like the weather station at your local airport. There are several good long term aggregators that harvest METAR data from these stations like this one at Iowa State, or you can get the most recent week of data by searching for your local airport code at weather.gov

METAR is a format for weather reporting that is predominately used for pilots and meteorologists and they report pressure adjusted to ‘Mean Sea Level’. So you will have to adjust your data to MSL (or reverse the correction on the airport data) before you can compare it to the pressure reported by your local sensors. For this you will also need to know the exact altitude of your sensors when the data was gathered to remove the height offset between your location and the airport stations.

Technically speaking, you could calibrate your pressure sensors directly to those official sources. However there are a lot of Beginner, Intermediate and Advanced details to take care of. Even then you still have to be close enough to know both locations are in the same weather system.

Here I’m just going to use the relatively crude adjustment equation:
Station Pressure = SLP – (elevation/9.2) and millibar = inchHg x 33.8639 to see if we are in the ballpark.

**Barometric data from the local airport** (16 miles away) **overlayed on our normalized pressure sensors**. It’s worth noting that the airport data is at a strange odd-minute intervals, with frequent dropouts which would complicate a calibration to that reference.

Like most pressure sensors an MS58xx also records temperature because it needs that for internal calculation. So we can repeat the entire process with the temperature readings from this sensor set:

Temperatures °C from a set of MS58xx Pressure sensors: before & after group normalization. Unlike pressure, this entire band was within the ±2ºC specified in the datasheet.

These sensors were sitting pretty far back on a bookshelf that was partly enclosed, so some of them were quite sheltered while others were exposed to direct airflow. So I’m not bothered by the spikes or the corresponding blips in those residual plots. I’m confident that if I had run this test inside a thermally controlled environment (ie: a styrofoam cooler with a small hole in the top) the temperature residuals would have been well behaved.

One of the loggers in this set had a calibrated NTC thermistor onboard. While this sensor had significant lag because it was located inside the housing, we can still use it to check if the normalized temperatures benefit from the same random distribution of errors that were corrected so nicely by the pressure normalization:

Once again, we have good alignment between a trusted reference (in red) and our normalized sensors.

Comments:

Normalization is a relatively low effort way to improve sets of sensors – and it’s vital if you are monitoring systems that are driven primarily by gradients rather than absolute values. This method generalizes to many other types of sensors although a simple y=Mx +B approach usually does not handle exponential sensors very well. As with calibration, the data set used for normalization should span the range of values you expect to gather with the sensors later on.

The method described here only corrects differences in Offset [with the B value] & Gain/Sensitivity [the M value] – more complex methods are needed to correct non-linearity problems. To have enough statistical power for accuracy improvement you want a batch of ten or more sensors and it’s a good idea to exclude data from the first 24 hours of operation so brand new sensors have time to settle. Offsets are influenced by several factors and some sensors need to ‘warm up’ before they can be read. The code driving your sensors during normalization should be identical to the code used to collect data in the field.

All sensor parameters drift so, just like calibration, normalization constants have a shelf life. This is usually about one year, but can be less than that if your sensors are deployed in harsh environments. Fortunately this kind of normalization is easy to redo in the field, and it’s a good way to spot sensors that need replacing. You could also consider airport/NOAA stations as stable references for drift determination.

References & Links:

Decoding Pressure @ Penn State
Environmental Mesonet @ Iowa State
Calibrating your Barometer: Part1, Part2 & Part3
How to Use Air Sensors: Air Sensor Guidebook
ISA Standard Atmosphere calculator
Starpath SLP calculator
SensorsONE Pressure Calculators
Mean Sea Level Pressure converter

How do you deal with I2C bus resistance/capacitance issues with so many sensors connected?

I have to add a special mention here of the heroic effort by liutyi comparing different temp. & humidity sensors. While his goal was not normalization, the graphs clearly demonstrate how important that would be if you were comparing a group of sensors. Humidity sensors have always been a thorn in our side – both for lack of inter-unit consistency and because of their short lifespan in the field relative to other types of sensors. The more expensive Sensirons tend to last longer – especially if they are inside one of those protective shells made from sintered metal beads. KanderSmith also did an extensive comparison of humidity sensors with more detailed analysis of things like sensor response time.

You can use the map function to normalize range sensors where both the upper and lower bounds of the sensor varies. And you can use Binary Saturated Aqueous Solutions as standards.

How to calibrate NTC thermistors (A DIY method you can do at home)

This post describes a thermistor calibration achievable by people who don’t have access to lab equipment with an accuracy better than ±0.15°C. This method is particularly suitable for the 10k NTC on our 2-module data logger handling them in a way that is easy to standardize for batch processing (ie: at the classroom scale). We use brackets to keep the loggers completely submerged because the thermal conductivity of the water around the housing is required or the two sensors would diverge. The target range of 0° to 40°C used here covers moderate environments including the underwater and underground locations we typically deploy into. This method is unique in that we use a freezing process rather than melting ice for the 0°C data point.

Use stainless steel washers in your hold-downs to avoid contamination of the distilled water and provide nucleation points to limit super-cooling. Before creating this bracket we simply used zip-ties to hold the washer weights.

Reading a thermistor with digital pins uses less power, and gives you the resistance of the NTC directly from the ratio of two Interrupt Capture Unit times. Resolution is not set by the bit depth of your ADC, but by the size of the reservoir capacitor: a small ceramic 0.1µF [104] delivers about 0.01°C with jitter in the main system clock imposing a second limit on resolution at nearly the same point. Large reservoir capacitors increase resolution and reduce noise but take more time and use more power. The calibration procedure described in this post will work no matter what method you use to read your NTC thermistor.

The I2C reference sensor is connected temporarily during the calibration via Dupont headers. Always give your reference sensors serial numbers so that you can normalize them before doing the thermistor calibrations.

Off-the-shelf sensors can be used as ‘good enough’ reference thermometers provided you keep in mind that most accuracy specifications follow a U-shaped curve around a sweet spot that’s been chosen for a particular application. The Si7051 used here has been optimized for the medical market, so it has ±0.1° accuracy from 35.8 to 41° Celsius, but that falls to ±0.13° at room temperatures and only ±0.25° at the ice point. If you use some other reference sensor (like the MAX30205 or the TSYS01) make sure it’s datasheet specifies how the accuracy changes over the temperature range you are targeting with the calibration.

The shortened Steinhart–Hart equation used here is not considered sufficiently accurate for bench-top instruments which often use a four or five term polynomial. However in ‘The Guide on Secondary Thermometry‘ by White et. al. (2014) the three-term equation is expected to produced interpolation errors of about 0.0025°C over a range from 0 to 50°C, and that is acceptable for most monitoring. To calculate the three equation constants you need to collect three temperature & resistance data pairs which can be entered into the online calculator at SRS or processed with a spreadsheet.

While these technical sources of error limit the accuracy you can achieve with this method, issues like thermal lag in the physical system and your overall technique are more important. In general, you want each step of the calibration process to occur as slowly as possible. If the data from a run doesn’t look the way you were expecting – then do the procedure over again until those curves are well behaved and smooth. Make sure the loggers stay dry during the calibration – switching to spare dry housing tubes between the baths: Moisture is the greatest cause of failure in sensors and humidity/water always lowers the resistance of thermistors. If in doubt, let everything dry for 24 hours before re-doing a calibration.

Data Point #1: The freezing point of water

The most common method of obtaining a 0°C reference is to place the sensor into an insulated bucket of stirred ice slurry that plateaus as the ice melts. This is fine for waterproof sensors on the end of a cable but it is not easily done with sensors mounted directly on a PCB. So we immerse the loggers in collapsible 1200ml silicone food containers filled with distilled water. This is placed inside of a well insulated lunch box and the combined assembly is left in the freezer overnight, reading every 30 seconds.

Weighted holders keep each logger completely immersed. Soft-walled silicone containers expand to accommodate any volume change as the water freezes. This prevents the centrifuge tube housings from being subjected to pressure as the ice forms. **Position the loggers so that they are NOT in direct contact with the sides or the lid of the silicone container**.

The outer box provides insulation to slow down the freezing process. After testing several brands it was found that the Land’s End EZ wipe (9″x8″x4″) and Pottery Barn Kids Mackenzie Classic lunch boxes provided the best thermal insulation because they have no seams on the solid molded foam interior which also doesn’t absorb water spilled while moving the containers around.

For the purpose of this calibration (at ambient pressure) we can treat the freezing point of pure water as a physical constant. So no reference sensor is needed on the logger while you collect the 0°C data. Leave the lunch box in the freezer just long enough for a rind of ice to form around the outer edges while the main volume of water surrounding the loggers remains liquid. I left the set in this photo a bit too long as that outer ice rind is much thicker than it needed to be for the data collection. Do not let the water freeze completely solid (!) as this will subject the loggers to stress that may crack the tubes and let water in to ruin your loggers.

The larger bubbles in this photo were not present during the freeze, but were created by moving the container around afterward for the photo.

The trick is recognizing which data represents the true freezing point of water. Distilled water super-cools by several degrees, and then rises to 0°C for a brief period after ice nucleation because the phase change releases 80 calories per gram while the specific heat capacity of water is only one calorie, per degree, per gram. So freezing at the outer edges warms the rest of the liquid – but this process is inherently self-limiting which gives you a plateau at exactly 0°C after the rise:

**NTC (ohms) gathered during the freeze/thaw process** graphed with the y axis is inverted because of the negative coefficient. The warm temperature data has been removed from the graphs above to display only the relevant cold-temperature data. Only the 10-20 minutes of data immediately after the rise from a super cooled state is relevant to the calibration. Cooling the insulated chamber from its room temperature starting point to the supercooling spike shown above took 7-8 hours.

Depending on the strength of your freezer, and the quality of the outer insulating container, the ice-point may only last a few minutes before temperatures start to fall again. An average of the NTC readings from that SHORT plateau immediately after the supercooling ends is your 0°C calibration point. This is usually around 33000 ohms for a 10k 3950 thermistor. Only the data immediately after super cooling ends is relevant and the box can be removed from the freezer any time after that event. I left the example shown above in the freezer too long but you have a reasonable window of time to avoid this. Once the freeze process initiates, it usually takes about 8 hours for the entire volume to freeze solid – after which you can see the compressor cycling as the now solid block cools below 0°C. You want to pull the sensors out of the freezer before that solid stair-step phase (at 8:00 above) if possible.

If the supercooling spike is not obvious in your data then change your physical configuration to slow the cooling process until it appears. You want the inner surface of your silicone container to have smooth edges, as sharp corners may nucleate the ice at 0°C, preventing the supercooling spike from happening. Use as much distilled water as the container will safely hold -the loggers should be surrounded by water on all sides.

In this image a freezer compressor cycle happened during post supercooling rise making it hard to see where the plateau occurred. This run was re-done to get better data.

Most refrigerators cycle based on how often the door is opened and those cycles can overprint your data making it hard to interpret. If you put a room-temperature box of water in the freezer between 6-7pm, it usually reaches the supercooling point around 2am, reducing the chances that someone will open the refrigerator/freezer door at the critical time. Even then, unexpected thermal excursions may happen if the freezer goes into a defrost cycle or an automatic ice-maker kicks in during the run. The time to reach that supercooling event can be reduced by pre-cooling the distilled water to ~5°C in the refrigerator before the freezer run. If any of the points on your curves are ambiguous, then do that run again, making sure the water is completely ice free at the start.

As a technical aside, the energy released (or absorbed) during the phase change of water is so much larger than its typical thermal content that water based heat pumps can multiply their output significantly by making slushies.

Data Point #2: Near 40°C

We have used the boiling point of water for calibration in the past, but the centrifuge tube housings would soften considerably at those temperatures. Ideally you want to bracket your data with equally spaced calibration points and 100°C is too far from the environmental conditions we are targeting. Heated water baths can be found on eBay for about $50, but my initial tests with a Fisher Scientific IsoTemp revealed thermal cycling that was far too aggressive to use for calibration – even with a circulation pump and many layers of added insulation. So we created an inexpensive DIY version made with an Arctic Zone Zipperless Coldloc hard-shell lunch box and a 4×6 inch reptile heating mat (8 watt). Unlike the ice point which must be done with distilled water, ordinary tap water can be used to collect the two warm temperature data pairs.

These hard-sided Arctic Zone lunch boxes can often be obtained for a few dollars at local charity shops or on eBay.

Place the 8-watt heating pad under the hard shell of the lunch box. **At 100% power** this tiny heater takes ~24 hours to bring the bath up to ~38°C. The **bath temp is relatively stable since the heater does not cycle**, but it does experience a slow drift based on losses to the environment. These heating pads sell for less than $15 on Amazon.

To record the temperature inside each logger, an Si7051 breakout module (from Closed Cube) is attached to the logger. A hold down of some kind must keep the logger completely submerged for the duration of the calibration. If a logger floats to the surface then air within the housing can thermally stratify and the two sensors will diverge. That data is not usable for calibration so the run must be done again with that logger.

The reference sensor needs to be as close to the NTC sensor as possible within the housing – preferably with the chip directly over top and facing the NTC thermistor.

Data Point #3: Room Temperature

The loggers stay in the heated bath for a minimum of 4 hours, but preferably 8 -12 hours. The idea is you want the whole assembly to have enough time to equilibrate. Then they are transferred to an unheated water-filled container (in this case a second Arctic Zone lunch box) where they run at ambient temperatures for another 8 -12 hours. This provides the final reference data pair:

**Si7051 temperature** readings inside a logger at a 30 second sampling interval. The logger was transferred between the two baths at 8am. Both baths are affected by the temperature changes in the external environment.

**Detail:** Warm temp. NTC ohms (y-axis inverted)

**Detail:** Room temp. NTC ohms (y-axis inverted)

As the environment around the box changes, losses through the insulation create gentle crests or troughs where the lag difference between the sensors will change sign. So averaging several readings across those inflection points cancels out any lag error between the reference sensor and the NTC. Take care that you average exactly the same set of readings from both the Si7051 and from the NTC. At this point you should have three Temperature / Resistance data pairs that can be entered into the SRS online calculator to calculate the equation constants ->

I generally use six digits from the reference pairs, which is one more than I’d trust in the temperature output later. I also record the Beta constants for live screen output because that low accuracy calculation takes less time on limited processors like the 328p.

The final step is to use those constants to calculate the temperature from the NTC data with:
Temperature °C = 1/(A+(B*LN(ohms))+(C*(LN(ohms))^3))-273.15

Then graph the calculated temperatures from the NTC calibration readings over top of the reference sensor temperatures. Provided the loggers were completely immersed in the water bath, flatter areas of the two curves should overlap one another precisely. However, the two plots will diverge when the temperature is changing rapidly because the NTC exhibits more thermal lag than the Si7051. This is because the NTC is located near the thermal mass of the ProMini circuit board.

**Si reference & NTC calculated temperatures:** If your calibration has gone well, the curves should be nearly identical as shown above. With exceptions only in areas where the temperature was changing rapidly and the two sensors got out of sync because of different thermal lags.

Also note that the hot and warm bath data points can be collected with separate runs. In fact, you could recapture any individual data pair and recalculate the equation constants with two older ones any time you suspect a run did not go smoothly. Add the constants to all of the data column headers, and record them in a google doc with the three reference pairs and the date of the calibration.

Validation

You should always do a final test to validate your calibrations, because even when the data is good it’s easy to make a typo somewhere in the process. Here, a set of nine calibrated NTC loggers are run together for a few days in a gently circulating water bath at ambient temperature –>

Two from this set are a bit high and could be recalibrated, but all of the NTC temperature readings now fall within a 0.1°C band. This is a decent result from a method you can do without laboratory grade equipment, and the sensors could be brought even closer together by using this validation data to normalize the set.

Comments

The method described above uses equipment small enough to be portable, allowing easy classroom setup/takedown. More importantly this also enables the re-calibration of loggers in the field if you have access to a freezer. This makes it possible to re-run the calibrations and then apply compensation techniques to correct for sensor drift. Validating calibration before and after each deployment is particularly important with DIY equipment to address questions about data quality at publication. Glass encapsulated NTC thermistors drift up to 0.02 °C per year near room temperatures, while epoxy coated sensors can drift up to 10x that.

At the ice-point, our resolution is ~0.0025°C but our time-based readings vary by ±0.0075°C. This is due to timing jitter in the ProMini oscillator and in the interrupt handling by a 328p. So with a [104] reservoir capacitor in the timing circuit, our precision at 0°C is 0.015°C.

Having a physical constant in the calibration data is important because most of the affordable reference sensors in the Arduino landscape were designed for applications like healthcare, hvac, etc. So they are usually designed minimize error in warmer target ranges, while getting progressively worse as you approach 0°C. But accuracy at those lower temperatures is important for environmental monitoring in temperate climates. The method described in this post could also be used to calibrate commercial temperature sensors if they are waterproof.

Calibrating the onboard thermistor a good idea even if you plan to add a dedicated temperature sensor because you always have to do some kind of burn-in testing on a newly built logger – so you might as well do something productive with that time. I generally record as much data as possible during the calibration to fill more memory and flag potentially bad areas in the EEprom. (Note: Our code on GitHub allows only 1,2,4,8, or 16 bytes per record to align with page boundaries) . And always look at the battery record during the calibration as it’s often your first clue that a DIY logger might not be performing as expected. It’s also worth mentioning that if you also save the RTC temperatures as you gather the NTC calibration data, this procedure gives you enough information to calibrate that register as well. The resolution is only 0.25°C, but it does give you a way to check if your ‘good’ temperature sensors are drifting because the DS3231 tends to be quite stable.

While the timing jitter does not change, non-linearity of the NTC resistance reduces the resolution to 0.005°C. Precision at 35°C also suffers, falling to 0.02°C. Using a 10x larger [105] reservoir cap would get us back to resolution we had at 0°C, as would oversampling which actually requires this kind of noise for the method to work. Either of those changes would draw proportionally more power from the coincell for each read so its a tradeoff that might not be worth making when you consider sensor lag.

For any sensor calibration the reference points should span the range you hope to collect later in the field. To extend this procedure for colder climates you could replace the ice point with the freezing point of Galinstan (-20°C) although a domestic freezer will struggle to reach that. If you need a high point above 40°C, you can use a stronger heat source. Using two of those 8 watt pads in one hard sided lunch box requires some non-optimal bending at the sides, but it does boost the bath temp to about 50°C. 3D printed PLA hold-downs will start to soften at higher temps so you may need to alter the design to prevent the loggers from popping out during the run.

If your NTC data is so noisy you can’t see where to draw an average, check the stability of your regulator because any noise on the rail will affect the Schmitt trigger thresholds used by our ICU/timer method. This isn’t an issue running from a battery, but even bench supplies can give you noise related grief if you’ve ended up with some kind of ground loop. You could also try oversampling, or a leaky integrator to smooth the data – but be careful to apply those techniques to both the reference and the NTC in exactly the same way because they introduce significant lag. Temperature maximums are underestimated and temperature minimums are overestimated by any factor that introduces lag into the system. In general, you want to do as little processing to raw sensor readings as possible at capture time because code-based techniques usually require some prior knowledge of the data range & variation before they can be used safely. Also note that our digital pin ICU based method for reading resistors does not work well with temperature compensated system oscillators because that compensation circuitry could kick in between the reference resistor and NTC readings.

And finally, the procedure described here is not ‘normalization’, which people sometimes confuse with calibration. In fact, it’s a good idea to huddle-test your sensors in a circulating water bath after calibration to bring a set closer together even though that may not improve accuracy. Creating post-calibration y=Mx+B correction constants is especially useful for sensors deployed along a transect, or when monitoring systems that are driven by relative deltas rather than by absolute temperatures. Other types of sensors like pressure or humidity have so much variation from the factory that they almost always need to be normalized before deployment – even on commercial loggers.

Normalize your set of reference sensors to each other before you start using them to calibrate NTC sensors.

References & Links:

SRS Online Thermistor Constant Calculator
Steinheart & Heart spreadsheet from CAS
S&H Co-efficient calculator from Inside Gadgets
Molex Experimenting with Thermistors Design Challenge
Thermistor Calibration & the Steinhart-Hart Equation WhitePaper from Newport
ITS-90 calibrates w Mercury(-38.83), Water(0.01) & Gallium(29.76) Triple Point cells
Guide on Secondary Thermistor Thermometry, White et al. (2014)
Steinhart-Hart Equation Errors BAPI Application Note Nov 11, 2015
The e360: A DIY Classroom Data Logger for Science
How to make Resistive Sensor Readings with DIGITAL I/O pins
Single Diode Temperature Sensors
Measuring Temperature with two clocks
How to Normalize a Set of Sensors